Introduction
This is one of the important topics in AP Physics C E&M.
Charge feels force on it. The force is dependent on the charge (q), velocity(v)and magnetic field (B).
![\[F=q(v \times B)\]](/wp-content/ql-cache/quicklatex.com-8bd28e16852d2f1c29185f9e4d4e4bb2_l3.png "Rendered by QuickLaTeX.com")
![\[\mathrm{F}=\mathrm{qvB} \sin \theta\]](/wp-content/ql-cache/quicklatex.com-5fabd168be33970d6c684cdde968bd4e_l3.png "Rendered by QuickLaTeX.com")
Let us consider this particle has a charge q and it moves in the direction of magnetic field B (motion in a magnetic field); the velocity is v and θ is the angle between B and V
We have different cases for a force experienced by a charge
CASE 1: if θ = 0 or 180
Velocity of charge is parallel or anti-parallel to magnetic field.
F= 0.
Trajectory = straight line.
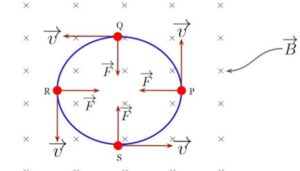
CASE 2: if θ = 90
Velocity of charge is perpendicular to magnetic field
![\[F=q v B \sin 90\]](/wp-content/ql-cache/quicklatex.com-020dd1c52aefb4c3153325f7b2c44965_l3.png "Rendered by QuickLaTeX.com")
![\[F=qvB\]](/wp-content/ql-cache/quicklatex.com-37866a62f8d7fa3f8eea477a2b0c6d09_l3.png "Rendered by QuickLaTeX.com")
F = F centripetal
Trajectory = circle (right-hand thumb rule )
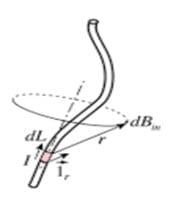
Biot savart law
Biot savart law is a fundamental relationship between an electric current I and the magnetic field B in physics.
Biot savart law equations describe the relationship between the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and electric current.
![\[d B=\frac{\mu_0 I d l \sin \theta}{4 \pi r^2}\]](/wp-content/ql-cache/quicklatex.com-5d847da63117401253a661b4af3faa30_l3.png "Rendered by QuickLaTeX.com")
dL = infinitesimal length of a conductor carrying electric current.
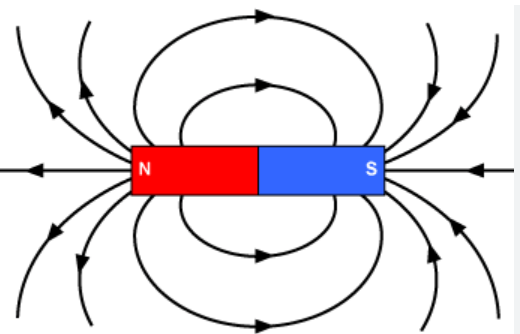
Magnetic Field
Magnetic Field is a region of space near a magnet.
In other words
A magnetic field is a field that describes the magnetic influence on moving electric charges and electric currents. A moving charge(q) in a magnetic field experiences a force perpendicular to its own velocity (v) and to the magnetic field. It can be denoted with B.
The electric field produced by a point charge q at rest at the origin is
![\[E=F / q\]](/wp-content/ql-cache/quicklatex.com-83446124576b774aeb3ed189d5a7460b_l3.png "Rendered by QuickLaTeX.com")
Where F is Electrostatics Force, and q is point charge.
Magnetic field lines
The magnetic field lines are a visual and intuitive realisation of the magnetic field.
The Dipole in a uniform magnetic field
The magnetic field lines give us an
approximate idea of the magnetic field (B). To
determine the magnitude of B accurately. This is done by placing a small compass needle of known magnetic moment (m) and moment of inertia (I)
and allowing it to oscillate in the magnetic field.
The torque on the needle is
![\[\tau=m \times B\]](/wp-content/ql-cache/quicklatex.com-6ba6fd16c617b29a6b0e74ccf6434b1c_l3.png "Rendered by QuickLaTeX.com")
In magnitude
![\[\tau=m B \sin \theta\]](/wp-content/ql-cache/quicklatex.com-30e0b59ad8e3d7d356c33e5aae0a62a1_l3.png "Rendered by QuickLaTeX.com")
Here τ is restoring torque and θ is the angle between m and B.
To know more about the other chapters tested in AP Physics C E&M, Check out Succeeding in AP Physics C Electricity and Magnetism
