Rate of Change in AP Precalculus

Rate of change Unit 1 topic 1.2 is a fundamental concept in mathematics, describing how a function’s $y$-coordinate changes with respect to its x-coordinate. In AP Precalculus, understanding rate of change is crucial—not only because it forms the foundation for later units in the course but also because it sets the stage for success in AP Calculus AB and BC.

In calculus, an entire semester is devoted to exploring derivatives, and the deeper relationships between rate of change and the behavior of functions. Grasping this concept early can make advanced topics like differentiation and integration much more approachable. You can also book an experienced and affordable private online AP Precalculus tutor.

Have you ever wondered why some graphs “smile” while others “frown”? Or how does the steepness of a curve tell us whether something is speeding up or slowing down? By the end of this blog, you’ll not only know the answers but also have the tools to ace Unit 1 of AP Precalculus – particularly 1.2 rate of change and its applications.

Positive and Negative Functions

Before discussing the rate of change, let’s first understand when a function itself is positive or negative.

• A function is positive whenever its y-coordinate is positive. In other words, the function lies above the x-axis on a graph.
• Conversely, a function is negative whenever its y-coordinate is negative, meaning the function is below the x-axis.

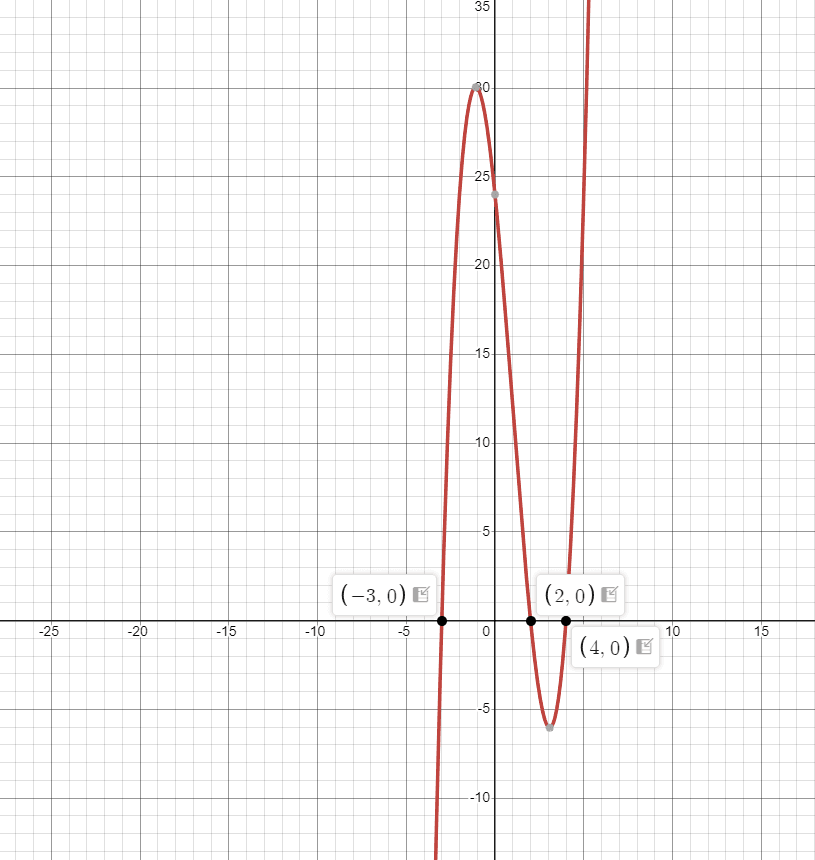
To visualize these concepts further, you can try out Desmos, an excellent graphing tool for students and educators. Consider a simple curve. Parts of the graph that are above the x-axis correspond to positive values of the function, while sections below the x-axis represent negative values.

In the above curve, function is positive in (-3,2)U(4,inf) while negative in (-inf,-3)U(2,4)

Positive and Negative Rate of Change

The rate of change of a function represents the slope of the tangent line drawn at any given point on the graph. Whether the rate of change is positive or negative depends on the slope of this tangent line and the behavior of the function.

• When the slope is positive, the tangent line makes an acute angle with the x-axis. This happens when the function is increasing—essentially, when the graph is climbing.
• When the slope is negative, the tangent line makes an obtuse angle with the x-axis. This occurs when the function is decreasing—or, to use the opposite of climbing, when the graph is descending.

To make this more intuitive:

• A positive rate of change corresponds to an upward-trending function.
• A negative rate of change corresponds to a downward-trending function.

In the above curve, the function is increasing in (-inf,-1.08)U(3.08,inf) while decreasing from (-1.08,3.08).
In other words, the function’s Rate of Change is positive in (-inf,-1.08)U(3.08,inf) while Rate of Change is negative from (-1.08,3.08).

Understanding the rate of change is foundational for future topics like derivatives. If you’re tackling Unit 2 in AP Precalculus, check out my blog on Unit 2 of AP Precalculus for more in-depth examples

When Is the Rate of Change Increasing or Decreasing?

The rate of change can itself be increasing or decreasing, and this ties directly to the concavity of the function:

• The rate of change is increasing when the graph forms a smiling face, also known as a concave up function.
• The rate of change is decreasing when the graph forms a frowning face, also known as a concave down function.

To make this connection clearer:

• A concave up function (smiling face) is often described as having an increasing rate.
• A concave down function (frowning face) is often described as having a decreasing rate.

In the above graph:

Rate of change is increasing OR function has an increasing rate OR function is concave up from (1,inf)

Rate of change is decreasing OR function has a decreasing rate OR function is concave down from (-inf,1)

For a deeper dive into AP Precalculus concepts, check out the official AP resources on the College Board website

To see a practical example of rate of change in action, watch the video below:

Rate of Rate of Change

The rate of rate of change refers to how the rate of change itself is behaving—whether it’s increasing or decreasing.

• When the rate of rate of change is positive, it means the rate of change is increasing. This corresponds to the function being concave up.
• When the rate of rate of change is negative, it means the rate of change is decreasing. This corresponds to the function being concave down.

To sum it up, all of these terms mean the same thing:

• Rate of change is increasing, rate of rate of change is positive, increasing rate, and concave up are interchangeable.
• Similarly, rate of change is decreasing, rate of rate of change is negative, decreasing rate, and concave down all mean the same thing.

Understanding this equivalence helps simplify complex problems and ensures you can approach them from multiple perspectives.

Conclusion

To sum up everything we’ve learned about rate of change and its behavior, here’s a quick recap of the key ideas and their synonyms:

• Function Positive or Negative:

  • A function is positive when its y-value is positive (above the x-axis).
  • A function is negative when its y-value is negative (below the x-axis).

• Rate of Change Positive or Negative:

  • A positive rate of change means the function is increasing, the tangent line has a positive slope, and the tangent makes an acute angle with the x-axis.
  • A negative rate of change means the function is decreasing, the tangent line has a negative slope, and the tangent makes an obtuse angle with the x-axis.

• Rate of Change Increasing or Decreasing:

  • Rate of change increasing is the same as:
    • Rate of rate of change positive
    • Increasing rate
    • Concave up
    • Smiling face
  • Rate of change decreasing is the same as:
    • Rate of rate of change negative
    • Decreasing rate
    • Concave down
    • Frowning face

To dive deeper into these concepts and see them in action, be sure to check out my YouTube video linked below!

To explore more AP Precalculus concepts and strengthen your understanding, check out our AP Precalculus YouTube playlist. Don’t forget to subscribe to our channel for more helpful videos like this one!

Frequently Asked Questions (FAQs)

Q. What are some good resources for AP Precalculus?

Here are some of the good resources that cater to different learning styles and needs:

1. Our collection of free downloadable AP Precalculus worksheets with solutions.
2. “Barron’s AP Precalculus” by David Bock M.S. and Dennis Donovan M.S.
3. “Precalculus: Mathematics for Calculus” by James Stewart, Lothar Redlin, and Saleem Watson

Q. Can I skip pre-calc and go to AP Calc?

Jumping directly into AP Calculus AB or AP Calculus BC without a solid foundation in Precalculus can make it difficult to secure even a B or C grade. It also significantly increases the likelihood of underperforming on the AP Calculus exam. Precalculus provides essential skills and concepts that are critical for success in AP Calculus, making it an important step in your math journey.

Ultimately, decisions about skipping Precalculus should be made carefully, considering your abilities and input from teachers. While some students may manage to transition directly to AP Calculus, a strong understanding of basic concepts is crucial for excelling in advanced math courses.