- I. Introduction: Brief overview of AP Precalculus Unit 3
-
- 3.6 Sinusoidal Function Transformations
- 3.7 Sinusoidal Function Context and Modeling
- 3.8 The Tangent Function
- 3.9 Inverse Trigonometric Functions
- 3.10 Trigonometric Equations and Inequalities
- 3.11 The Secant, Cosecant, and Cotangent Functions
- 3.12 Equivalent Representations of Trigonometric Functions
- 3.13 Trigonometry and Polar Coordinates
- 3.14 Polar Function Graphs
- 3.15 Rates of Change in Polar Functions
- II AP Precalculus unit 3 Practice
I. Introduction: Brief overview of AP Precalculus Unit 3
In Unit 3 of AP Precalculus, students will dive into the fundamental concepts of trigonometry. We already know about functions from Unit 1. This unit now focuses on developing a deep understanding of trigonometric functions and their properties. Students will explore topics such as angles, radians, degrees, and the unit circle. They will learn how to evaluate trigonometric functions, solve trigonometric equations, and manipulate trigonometric expressions. Additionally, this unit covers the graphs of trigonometric functions, including sine, cosine, and tangent, and their transformations. Practical applications of trigonometry, such as modeling periodic phenomena and solving real-world problems involving angles and triangles, are also discussed. Throughout the unit, students will engage in various exercises and problems to reinforce their understanding of trigonometric concepts and their applications. We learnt how to do regression analysis of logs and exponents in Unit 2. In this unit, we will learn the same for Trigonometric functions. By the end of Unit 3, students will have acquired a solid foundation in trigonometry that will prepare them for more advanced mathematical studies. This unit requires about 7-10 weeks of prep time and covers 30-35% of AP Exam weightage. This is the last unit tested in AP. Unit 4 is not a part of AP Precalculus.
3.1 Periodic Phenomena
In Section 3.1, students will explore the concept of periodic phenomena. This section introduces the idea of events or behaviors that repeat over regular intervals. Examples of periodic phenomena encountered in everyday life include the changing seasons, the motion of a pendulum, and the oscillation of a spring. Students will learn to identify periodic patterns in data sets and represent them using mathematical models, particularly sinusoidal functions. By understanding the characteristics of periodic phenomena, students can analyze and predict various natural and man-made processes. Through practical examples and problem-solving exercises, students will develop proficiency in recognizing, describing, and analyzing periodic behavior, laying the groundwork for more advanced applications in trigonometry and calculus.
3.2 Sine, Cosine, and Tangent
In Section 3.2, students will learn the fundamental trigonometric functions: sine, cosine, and tangent. These functions are essential tools for analyzing and understanding the relationships between angles and sides in right triangles. Through practical examples, students will learn how to evaluate trigonometric functions for specific angles, both in degrees and radians. Additionally, they will explore the graphical representations of these functions, gaining insight into their periodic nature and properties. Understanding sine, cosine, and tangent functions is crucial for solving various problems in fields such as engineering, physics, and astronomy. By mastering these foundational concepts, students will develop the skills needed to tackle more complex trigonometric topics and real-world applications with confidence.
3.3 Sine and Cosine Function Values
In Section 3.3, students will focus on understanding the values of sine and cosine functions for various angles. These functions represent the ratios of the lengths of sides in right triangles. They will explore the unit circle as a tool for visualizing these values and understanding their periodic nature. Additionally, students will discover how to use reference angles to find the sine and cosine values of angles beyond the primary interval. By mastering the sine and cosine function values, students will develop a solid foundation for solving trigonometric equations
3.4 Sine and Cosine Function Graphs
In Section 3.4, students will explore the graphs of sine and cosine functions. These graphs provide valuable visual representations of the behavior of these trigonometric functions across different angles. Through straightforward explanations and illustrative examples, students will learn to identify key features of sine and cosine graphs, such as amplitude, period, phase shift, and vertical displacement. Additionally, students will compare and contrast the graphs of sine and cosine functions, recognizing their similarities and differences. By mastering the graphical representations of sine and cosine functions, students will gain insight into the periodic nature of trigonometric phenomena and develop the skills necessary to analyze and solve a wide range of trigonometric problems.

3.5 Sinusoidal Functions
In Section 3.5, students will study sinusoidal functions, which are mathematical representations of periodic phenomena characterized by the sine and cosine functions. These functions exhibit specific properties that are essential for understanding their behavior and applications. We already introduced some other functions while giving and overall overview on AP Precalculus. However, The sine function, denoted as ![]() , oscillates between -1 and 1, reaching its maximum and minimum values at regular intervals. It has a period of
, oscillates between -1 and 1, reaching its maximum and minimum values at regular intervals. It has a period of ![]() radians and is symmetric about the origin. The cosine function, denoted as
radians and is symmetric about the origin. The cosine function, denoted as ![]() , shares similar properties with the sine function but is shifted horizontally by
, shares similar properties with the sine function but is shifted horizontally by ![]() radians. Both sine and cosine functions are periodic, with a period of
radians. Both sine and cosine functions are periodic, with a period of ![]() radians, and exhibit sinusoidal behavior.
radians, and exhibit sinusoidal behavior.
The graphs of sine and cosine functions are closely related, as they represent different aspects of the same periodic phenomena. The sine function graph resembles a wave that starts at the origin, reaches its maximum value at ![]() , crosses the x-axis at
, crosses the x-axis at ![]() , reaches its minimum value at
, reaches its minimum value at ![]() , and returns to the origin after completing one full period. On the other hand, the cosine function graph is similar to the sine function graph but is horizontally shifted to the left by
, and returns to the origin after completing one full period. On the other hand, the cosine function graph is similar to the sine function graph but is horizontally shifted to the left by ![]() radians. It starts at
radians. It starts at ![]() , crosses the x-axis at
, crosses the x-axis at ![]() , reaches its minimum value at
, reaches its minimum value at ![]() , and returns to its maximum value at
, and returns to its maximum value at ![]() .
.
3.6 Sinusoidal Function Transformations
In Section 3.6, students will explore transformations of sinusoidal functions through adjustments in horizontal and vertical shifts, changes in period, modifications in midline, and phase shifts. These alterations allow for tailoring sinusoidal functions to match specific patterns or accurately model various phenomena.
Horizontal shifts involve moving the graph of a sinusoidal function left or right along the x-axis, affecting its phase shift. Vertical shifts entail shifting the entire graph up or down along the y-axis, changing its midline. Changing the period adjusts the distance between consecutive maximas or minimas of the function. Phase shifts modify the start position of the function, horizontally along the x-axis, without altering its period or midline.
3.7 Sinusoidal Function Context and Modeling
In Section 3.7, students explore the application of sinusoidal functions in real-world contexts and modeling. Sinusoidal functions are particularly useful for modeling periodic phenomena, such as the motion of a pendulum or a Ferris wheel. By representing these phenomena with sinusoidal waveforms, students can analyze and predict their behavior more effectively.
For example, the motion of a pendulum can be modeled using a sinusoidal function, where the angle of the pendulum changes sinusoidally as it swings back and forth. Similarly, the height of riders on a Ferris wheel as it rotates can be described by a sinusoidal function, with the height varying periodically as the wheel turns.
Understanding how to model real-life problems with sinusoidal functions is crucial for success in AP Precalculus, as it prepares students for Free Response Question (FRQ) Type 3, which often involves applying Precalculus concepts to real-world scenarios.
3.8 The Tangent Function
In Section 3.8 of the AP Precalculus curriculum, students explore the tangent function, a fundamental trigonometric function with distinct properties. The tangent function, denoted as tan(x), represents the ratio of the sine of an angle to the cosine of the same angle in a right triangle. One key property of the tangent function is that it is undefined at certain angles where the cosine of the angle is zero, resulting in vertical asymptotes in its graph. Additionally, the tangent function has a period of 𝜋 radians and repeats its values every π radians.
The graph of the tangent function exhibits a repeating pattern, with vertical asymptotes occurring at regular intervals. The function approaches positive or negative infinity as it approaches these asymptotes, depending on the direction of the function’s approach. Moreover, the graph is symmetric about the origin, with identical shapes occurring in each quadrant of the coordinate plane.
Understanding the properties of the tangent function is essential for solving trigonometric equations and analyzing real-world problems involving angles and triangles.
3.9 Inverse Trigonometric Functions
In Section 3.9 of the AP Precalculus, students explore inverse trigonometric functions, which are functions that “undo” the effects of trigonometric functions. The most common inverse trigonometric functions are arcsin(x), arccos(x), and arctan(x), denoting the inverse of the sine, cosine, and tangent functions, respectively. These functions have restricted domains to ensure that they are one-to-one, meaning that each input corresponds to exactly one output. For example, the domain of the arcsine function is restricted to the interval [-1, 1], as the range of the sine function is [-1, 1].
One key property of inverse trigonometric functions is that they return angles rather than ratios of side lengths in a right triangle. The outputs of inverse trigonometric functions are measured in radians and represent the angle whose sine, cosine, or tangent matches the input value
By mastering inverse trigonometric functions, students develop the skills needed to analyze and interpret trigonometric relationships and apply them in real-world contexts.
Curious about reliable resources of AP Precalculus? Checkout Top 10 books for AP Precalculus
3.10 Trigonometric Equations and Inequalities
In Section 3.10 of the AP Precalculus curriculum, students get into trigonometric equations and inequalities, learning how to solve for general solutions. When solving trigonometric equations, students often encounter angles that satisfy the equation over a specified interval. To find the general solution, they identify all possible angles that satisfy the equation within the given interval, taking into account the periodic nature of trigonometric functions. For example, when solving ![]() over the interval
over the interval ![]() , students would find that
, students would find that ![]() and
and ![]() satisfy the equation within the interval. However, since sine is periodic with a period of
satisfy the equation within the interval. However, since sine is periodic with a period of ![]() , additional solutions exist beyond the given interval, such as
, additional solutions exist beyond the given interval, such as ![]() and
and ![]() , where
, where ![]() is an integer.
is an integer.
Similarly, when solving trigonometric inequalities, students must consider all possible solutions within the specified domain. They use algebraic techniques to isolate the variable and then analyze the intervals where the inequality is satisfied, often employing the unit circle or trigonometric identities to simplify expressions. By understanding how to find general solutions to trigonometric equations and inequalities, students gain insight into the behavior of trigonometric functions and develop problem-solving skills that are applicable across various disciplines.
3.11 The Secant, Cosecant, and Cotangent Functions
In Section 3.11 of the AP Precalculus curriculum, students explore the secant, cosecant, and cotangent functions, which are reciprocal trigonometric functions of cosine, sine, and tangent, respectively. The secant function, denoted as sec(x), is the reciprocal of the cosine function, while the cosecant function, denoted as csc(x), is the reciprocal of the sine function. Similarly, the cotangent function, denoted as cot(x), is the reciprocal of the tangent function. These functions are related to their counterparts sine, cosine, and tangent through their reciprocal relationships.
One key property of secant, cosecant, and cotangent functions is their period. Like their counterparts, they have a period of ![]() ,
, ![]() , and
, and ![]() radians respectively.
radians respectively.
3.12 Equivalent Representations of Trigonometric Functions
In Section 3.12 of the AP Precalculus curriculum, students explore equivalent representations of trigonometric functions, which encompass a variety of important identities that relate different trigonometric functions to one another. These identities include reciprocal identities, Pythagorean identities, sum and difference identities, double angle identities, and half angle identities.
Reciprocal identities express the relationships between trigonometric functions and their reciprocals, such as ![]() and
and ![]() . Pythagorean identities, such as
. Pythagorean identities, such as ![]() , relate the squares of sine and cosine functions to each other in a right triangle. Sum and difference identities, such as
, relate the squares of sine and cosine functions to each other in a right triangle. Sum and difference identities, such as ![]() , allow for the expression of the sine and cosine of sums and differences of angles.
, allow for the expression of the sine and cosine of sums and differences of angles.
Double angle identities, such as ![]() and
and ![]() , express the sine and cosine of double angles in terms of sine and cosine functions of single angles. Half angle identities, such as
, express the sine and cosine of double angles in terms of sine and cosine functions of single angles. Half angle identities, such as ![]() and
and ![]() , allow for the expression of the sine and cosine of half angles in terms of sine and cosine functions of single angles.
, allow for the expression of the sine and cosine of half angles in terms of sine and cosine functions of single angles.
FRQ Type 4 has one question based on this topic.
3.13 Trigonometry and Polar Coordinates
In Section 3.13 of the AP Precalculus curriculum, students explore trigonometry in polar coordinates, which provides an alternative way to represent points and shapes in the plane using angles and distances. In polar coordinates, each point is defined by its distance from the origin (referred to as the pole) and the angle it makes with the polar axis (typically the positive x-axis). The polar axis serves as the reference direction for measuring angles, similar to the x-axis in rectangular coordinates.
To plot a polar point, students can use the rectangular-to-polar conversion method. In this method, the following formulas can be used ![]() and
and ![]() to convert rectangular coordinates (x, y) to polar coordinates (r, θ).
to convert rectangular coordinates (x, y) to polar coordinates (r, θ).
In polar coordinates, a sign convention is used to determine the direction of angles and distances. Angles measured counterclockwise from the polar axis are typically considered positive, while those measured clockwise are negative.
On this topic, it is unlikely to get an FRQ, however AP Precalculus exam can grill students on MCQs.

3.14 Polar Function Graphs
In Section 3.14 of the AP Precalculus curriculum, students explore polar function graphs, which represent curves and shapes defined in polar coordinates. This is a very important topic of AP Calculus BC.
Various types of polar curves include:
- Limaçons: Curves with various shapes depending on parameters, defined by equations like
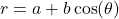 or
or 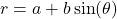 . Limacons could be Caridiod, Innerloop, Dimpled or Convex.
. Limacons could be Caridiod, Innerloop, Dimpled or Convex. - Roses: Curves with petal-like shapes, defined by equations like
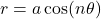 or
or 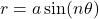 , where
, where 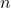 is an integer.
is an integer. - Lemniscates: Curves resembling infinity symbols, defined by equations like
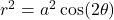 or
or 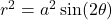 .
. - Spirals: Curves that wind around the origin, defined by equations like
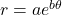 or
or 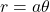 .
. - Circles: Curves consisting of all points equidistant from a fixed center point, defined by the equation
 ,
, 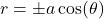 or
or 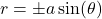 .
.
These are just a few examples of the diverse range of polar curves that can be encountered in mathematics. Each type of curve has its unique characteristics and equations, offering rich opportunities for exploration and study in polar coordinate systems.
Although the AP Precalculus exam does not typically require students to graph polar curves, they can still use elimination strategies to answer multiple-choice questions effectively. By understanding the characteristics of different types of polar graphs, students can eliminate incorrect answer choices and narrow down their options to arrive at the correct answer.
Additionally, students can use knowledge of symmetry and periodicity to eliminate incorrect options. For example, if a polar equation represents a graph with symmetry about the polar axis, students can eliminate answer choices that do not exhibit this symmetry.
By applying these elimination strategies, students can improve their chances of selecting the correct answer, even when they are not required to graph polar curves directly. This can maximize their performance on the AP Precalculus exam.
3.15 Rates of Change in Polar Functions
In polar functions, the formula for average rate of change in terms of polar functions can be expressed as:
![]()
where ![]() and
and ![]() are the values of the radius function at two different angles
are the values of the radius function at two different angles ![]() and
and ![]() within the interval, and
within the interval, and ![]() represents the change in angle.
represents the change in angle.
This formula calculates the average rate at which the radius changes over the given interval of angle. It provides a measure of how quickly or slowly the distance from the origin changes as the angle progresses along the curve. By evaluating the average rate of change at different intervals, one can gain insights into the overall behavior and dynamics of the polar curve.
To intuitively find the rate of change from a given graph, one can observe how the distance from the origin changes as the angle increases or decreases. If the graph appears to be steep, the rate of change is high, indicating rapid changes in the radius. Conversely, if the graph appears to be shallow, the rate of change is low, indicating slower changes in the radius.
For example, if we have a polar curve that forms a loop, the rate of change will be high as the curve sharply changes direction around the loop. Conversely, if the polar curve forms a spiral, the rate of change will be lower and more gradual as the curve spirals outward or inward.
II AP Precalculus unit 3 Practice
Looking for practice questions on AP Precalculus Unit 2? Share your details and get a free copy of worksheet.