-
I. Introduction: Brief overview of AP Precalculus Unit 4
- 4.1 Parametric Functions
- 4.2 Parametric Functions Modeling Planar Motion
- 4.3 Parametric Functions and Rates of Change
- 4.4 Parametrically Defined Circles and Lines
- 4.5 Implicitly Defined Functions
- 4.6 Conic Sections
- 4.7 Parametrization of Implicitly Defined Functions
- 4.8 Vectors
- 4.9 Vector-Valued Functions
- 4.10 Matrices
- 4.11 The Inverse and Determinant of a Matrix
- 4.12 Linear Transformations and Matrices
- 4.13 Matrices as Functions
- 4.14 Matrices Modeling Contexts
I. Introduction: Brief overview of AP Precalculus Unit 4
Unit 4 of AP Precalculus covers various advanced topics such as parametric equations, vector-valued functions, conic sections, and matrices. Parametric equations involve representing the coordinates of a point in terms of an independent parameter, offering a versatile way to describe complex curves and motions. Vector-valued functions extend the concept of functions to multiple dimensions, providing a powerful tool for describing motion and forces in physics and engineering. Conic sections study the geometric shapes formed by the intersection of a plane with a cone, including circles, ellipses, parabolas, and hyperbolas. Matrices introduce the fundamental concepts of linear algebra, including operations such as addition, multiplication, and inversion, which find applications in various fields including computer graphics and cryptography. It’s important to note that while Unit 1, Unit 2, and Unit 3 are tested on the AP exam administered by the College Board, Unit 4 is not directly assessed. However, individual schools may choose to include Unit 4 topics in their own exams as part of their AP Precalculus curriculum, providing students with a comprehensive understanding of advanced mathematical concepts.
4.1 Parametric Functions
We already discussed about Functions in Unit 1. In Unit 4.1 of AP Precalculus, students learn the concepts of parametric functions. Parametric functions offer a unique approach to describing curves and shapes by expressing the coordinates of a point as functions of an independent parameter, usually denoted as 𝑡. This allows for the representation of intricate curves and motions that cannot be easily described by traditional Cartesian functions. Parametric functions find applications in various fields such as physics, engineering, and computer graphics, where they are used to model the motion of particles, trajectories of projectiles, and the shape of complex curves.
4.2 Parametric Functions Modeling Planar Motion
Parametric functions play a vital role in modeling planar motion, allowing us to describe the movement of objects in a two-dimensional space over time. In unit 4.2 of AP Precalculus, students dive into the application of parametric equations to model various types of motion, such as the trajectory of projectiles, the motion of vehicles, or the path of a swinging pendulum. By parameterizing both the 𝑥 and 𝑦 coordinates as functions of time, we gain a flexible framework to represent complex motion patterns accurately. For example, when modeling the motion of a projectile launched at an angle to the horizontal, the 𝑥 and 𝑦 components of its position can be described separately as functions of time using parametric equations.
4.3 Parametric Functions and Rates of Change
In AP Precalculus Unit 4.3, students explore the relationship between parametric functions and rates of change. This is similar to what we discussed in Unit 2 and can be build on it. Parametric functions, which express the coordinates of a point as functions of an independent variable (usually time), allow us to analyze the behavior of objects in motion.
- Formula for the average rate of change of
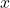 with respect to
with respect to 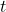 :
:
![]()
- Formula for the average rate of change of
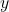 with respect to
with respect to 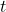 :
:
![]()
These formulas calculate the average rate of change of ![]() and
and ![]() over the interval
over the interval ![]() with respect to the parameter
with respect to the parameter ![]() . They provide insight into the overall change in
. They provide insight into the overall change in ![]() and
and ![]() per unit change in
per unit change in ![]() over the given interval.
over the given interval.
These rates of change provide crucial insights into the velocity and acceleration of moving objects. By studying how these rates of change vary with time, students can gain a deeper understanding of the dynamics of motion.
4.4 Parametrically Defined Circles and Lines
In Unit 4.4 of AP Precalculus, students study parametrically defined circles and lines. This section introduces parametric equations that describe the motion of points along circles and lines in the coordinate plane
Suppose we have a line in the Cartesian plane passing through two points, ![]() and
and ![]() . We can parameterize this line using the equations:
. We can parameterize this line using the equations:
![]()
![]()
Here, ![]() is the parameter that determines points along the line. When
is the parameter that determines points along the line. When ![]() , the point corresponds to
, the point corresponds to ![]() , and when
, and when ![]() , the point corresponds to
, the point corresponds to ![]() . Intermediate values of
. Intermediate values of ![]() generate points between these two endpoints.
generate points between these two endpoints.
For instance, if ![]() and
and ![]() , the parametric equations become:
, the parametric equations become:
![]()
![]()
These equations represent a line passing through the points (1, 2) and (4, 5). Varying the parameter ![]() allows us to trace out different points along this line segment, demonstrating the versatility and usefulness of parametric equations in describing geometric objects.
allows us to trace out different points along this line segment, demonstrating the versatility and usefulness of parametric equations in describing geometric objects.
Here’s an example for parametric equation of circle:
![Rendered by QuickLaTeX.com \[ \begin{cases} x = r \cos(t) \\ y = r \sin(t) \end{cases} \]](/wp-content/ql-cache/quicklatex.com-859923df75f71315ef41c6f8a6017c2e_l3.png)
where ![]() is the radius of the circle and
is the radius of the circle and ![]() is the parameter.
is the parameter.
4.5 Implicitly Defined Functions
Unit 4.5 of AP Precalculus introduces implicitly defined functions, which are functions whose equations don’t explicitly solve for 𝑦 in terms of 𝑥. Instead, they are represented by equations where 𝑦 and 𝑥 are intertwined. While these functions might not be directly expressed in terms of 𝑦 or 𝑥, they still define relationships between them.
Sure, let’s consider the implicitly defined function given by the equation:
![]()
This equation represents a curve known as the “Folium of Descartes.” While it may not be immediately apparent how ![]() depends on
depends on ![]() , each point
, each point ![]() that satisfies this equation lies on the curve.
that satisfies this equation lies on the curve.
Curious about reliable resources of AP Precalculus? Checkout Top 10 books for AP Precalculus
4.6 Conic Sections
Conic sections are geometric shapes formed by the intersection of a plane and a cone. In precalculus, we study three main types of conic sections: parabolas, ellipses, and hyperbolas. Each of these conic sections has a unique general equation that describes its shape.
A parabola, for instance, has a general equation of ![]() or
or ![]() , depending on whether it opens vertically or horizontally. If a parabola opens upwards or downwards along the y-axis, the general equation is
, depending on whether it opens vertically or horizontally. If a parabola opens upwards or downwards along the y-axis, the general equation is ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are constants. Similarly, if the parabola opens to the right or left along the x-axis, the equation becomes
are constants. Similarly, if the parabola opens to the right or left along the x-axis, the equation becomes ![]() .
.
Ellipses, on the other hand, have a general equation of ![]() if they are horizontally oriented or
if they are horizontally oriented or ![]() if they are vertically oriented. Here,
if they are vertically oriented. Here, ![]() represents the center of the ellipse, and
represents the center of the ellipse, and ![]() and
and ![]() are the semi-major and semi-minor axes, respectively.
are the semi-major and semi-minor axes, respectively.
Hyperbolas have a general equation of ![]() if they are horizontally oriented or
if they are horizontally oriented or ![]() if they are vertically oriented. Similar to ellipses,
if they are vertically oriented. Similar to ellipses, ![]() represents the center of the hyperbola, and
represents the center of the hyperbola, and ![]() and
and ![]() are the distances from the center to the vertices along the transverse and conjugate axes, respectively.
are the distances from the center to the vertices along the transverse and conjugate axes, respectively.
Understanding these general equations helps in identifying and graphing different conic sections, providing insight into their shapes and properties.
4.7 Parametrization of Implicitly Defined Functions
Parametrization of implicitly defined functions involves expressing the coordinates of a point on a curve using parameters. For parabolas, ellipses, and hyperbolas, this parametrization can be achieved through trigonometric functions – about which we have already discussed in Unit 3.
For a parabola, the parametric equations are ![]() ,
, ![]() , where
, where ![]() is a constant. These equations represent the motion of a point along the parabolic curve as a parameter
is a constant. These equations represent the motion of a point along the parabolic curve as a parameter ![]() varies.
varies.
Similarly, for an ellipse, the parametric equations are ![]() ,
, ![]() , where
, where ![]() and
and ![]() are the semi-major and semi-minor axes, respectively. Here,
are the semi-major and semi-minor axes, respectively. Here, ![]() varies from 0 to
varies from 0 to ![]() radians, covering one complete revolution around the ellipse.
radians, covering one complete revolution around the ellipse.
For a hyperbola, the parametric equations are ![]() ,
, ![]() . These equations describe the motion of a point along the hyperbolic curve as the parameter
. These equations describe the motion of a point along the hyperbolic curve as the parameter ![]() changes.
changes.
Understanding and using these parametric equations allow for a systematic approach to studying and analyzing the behavior of implicitly defined functions, providing insight into their geometric properties and relationships.
4.8 Vectors
Vectors are mathematical entities that represent quantities with both magnitude and direction. In simple terms, they are arrows drawn in space, each having a specific length and pointing in a particular direction. The magnitude of a vector is its length, while the direction indicates the path it follows. Vectors can be represented geometrically or algebraically.
When adding two vectors, the resultant vector is obtained by placing the tail of the second vector at the head of the first vector and drawing an arrow from the tail of the first vector to the head of the second vector. This process is known as vector addition. The sum of two vectors is another vector with a magnitude and direction determined by the individual vectors being added.
Parallel vectors have the same direction but may differ in magnitude. They lie on the same line or are co-linear. Conversely, anti-parallel vectors have the same magnitude but opposite directions, pointing in opposite directions along the same line.
Understanding vectors and their basic operations is essential in various fields. They are used to represent physical quantities such as displacement, velocity, and force, making them indispensable tools in analyzing and solving problems involving motion, forces, and other physical phenomena.
4.9 Vector-Valued Functions
Vector-valued functions are mathematical functions that output vectors instead of scalars. They are commonly used to describe motion in two or three dimensions, where each component of the vector represents a different aspect of the motion. For example, in the context of position, a vector-valued function ![]() describes the position of a particle at time
describes the position of a particle at time ![]() , with
, with ![]() and
and ![]() representing the horizontal and vertical components of the position, respectively.
representing the horizontal and vertical components of the position, respectively.
The sign of ![]() and
and ![]() indicates the direction of motion along the horizontal and vertical axes, respectively. If
indicates the direction of motion along the horizontal and vertical axes, respectively. If ![]() is positive, the particle is moving to the right. If
is positive, the particle is moving to the right. If ![]() is positive, the particle is moving up. Similarly, the magnitude of the vector
is positive, the particle is moving up. Similarly, the magnitude of the vector ![]() represents the distance from the origin to the point corresponding to the particle’s position at time
represents the distance from the origin to the point corresponding to the particle’s position at time ![]() .
.
In addition to position, vector-valued functions can also describe other aspects of motion, such as velocity and acceleration. For example, the velocity vector ![]() describes the instantaneous velocity of the particle at time
describes the instantaneous velocity of the particle at time ![]() , with
, with ![]() and
and ![]() representing the horizontal and vertical components of the velocity, respectively.
representing the horizontal and vertical components of the velocity, respectively.
4.10 Matrices
Matrices are mathematical objects that consist of rows and columns of numbers arranged in a rectangular array. They are commonly used to represent data, solve systems of linear equations, and perform transformations in geometry and computer graphics. The general format of a matrix is represented as follows:
![Rendered by QuickLaTeX.com \[ A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \]](/wp-content/ql-cache/quicklatex.com-8a8dc139114e5bb04e7d9e94953aaaba_l3.png)
In this format, the matrix ![]() has
has ![]() rows and
rows and ![]() columns, where each entry
columns, where each entry ![]() represents the element in the
represents the element in the ![]() -th row and
-th row and ![]() -th column of the matrix.
-th column of the matrix.
To multiply two matrices ![]() and
and ![]() , the number of columns in matrix
, the number of columns in matrix ![]() must be equal to the number of rows in matrix
must be equal to the number of rows in matrix ![]() . If
. If ![]() is an
is an ![]() matrix and
matrix and ![]() is an
is an ![]() matrix, then their product
matrix, then their product ![]() will be an
will be an ![]() matrix. The product
matrix. The product ![]() is obtained by taking the dot product of each row of matrix
is obtained by taking the dot product of each row of matrix ![]() with each column of matrix
with each column of matrix ![]() , where the entry in the resulting matrix at position
, where the entry in the resulting matrix at position ![]() is the sum of the products of the corresponding elements in the
is the sum of the products of the corresponding elements in the ![]() -th row of matrix
-th row of matrix ![]() and the
and the ![]() -th column of matrix
-th column of matrix ![]() .
.
4.11 The Inverse and Determinant of a Matrix
The inverse and determinant of a matrix are fundamental concepts in linear algebra. A square matrix is a matrix with the same number of rows and columns. The determinant of a square matrix is a scalar value that represents the matrix’s “scaling factor” when used in transformations or solving systems of linear equations. An inverse of a square matrix exists if and only if its determinant is non-zero. The inverse of a matrix is another matrix that, when multiplied together, results in the identity matrix.
For a 2×2 matrix ![]() , the determinant
, the determinant ![]() determines if an inverse exists. If the determinant is non-zero, the inverse exists, and it is given by:
determines if an inverse exists. If the determinant is non-zero, the inverse exists, and it is given by:
![]()
This formula involves swapping the positions of ![]() and
and ![]() , changing the signs of
, changing the signs of ![]() and
and ![]() , and dividing each entry by the determinant. The inverse of a matrix allows us to solve systems of linear equations and perform various transformations efficiently.
, and dividing each entry by the determinant. The inverse of a matrix allows us to solve systems of linear equations and perform various transformations efficiently.
4.12 Linear Transformations and Matrices
Linear transformations and matrices are essential concepts in mathematics, particularly in linear algebra. A linear transformation is a function that maps vectors from one space to another while preserving certain properties, such as linearity and the origin. Matrices provide a concise way to represent and analyze linear transformations. Each linear transformation corresponds to a unique matrix, and vice versa.
When a linear transformation is applied to a vector, it is equivalent to multiplying the vector by a certain matrix. This matrix represents how the transformation affects the vector’s coordinates. For example, a rotation transformation in the plane can be represented by a specific 2×2 matrix, and a scaling transformation can be represented by a diagonal matrix.
Matrices also facilitate the composition of linear transformations. When two linear transformations are applied sequentially, their corresponding matrices are multiplied together to form the matrix of the composite transformation. This process enables us to understand and analyze complex transformations more easily.
Furthermore, matrices provide a powerful tool for solving systems of linear equations. By representing a system of equations as a matrix equation, we can use matrix operations to solve for the unknown variables efficiently.
4.13 Matrices as Functions
Matrices can be viewed as functions that transform one vector space into another. When we consider a matrix as a function, its input is a vector, and its output is another vector. The transformation is achieved by multiplying the input vector by the matrix.
For example, let’s say we have a 2×2 matrix ![]() . We can interpret this matrix as a function that takes a 2-dimensional vector
. We can interpret this matrix as a function that takes a 2-dimensional vector ![]() as input and produces another 2-dimensional vector
as input and produces another 2-dimensional vector ![]() as output.
as output.
This viewpoint allows us to understand various properties of matrices in terms of functions. For instance, the determinant of a matrix corresponds to the scale factor by which the matrix stretches or compresses space. If the determinant is zero, the matrix collapses space onto a lower-dimensional subspace, and the matrix is said to be singular.
Furthermore, matrices can be combined and composed just like functions. When we multiply two matrices, we are essentially composing the corresponding functions. This composition corresponds to applying one transformation followed by another, resulting in a single combined transformation.
4.14 Matrices Modeling Contexts
Matrices find wide applications in modeling various real-world contexts across different fields, including physics, economics, engineering, and computer science. One common application is in systems of linear equations, where matrices are used to represent the coefficients of the equations and solve for unknown variables efficiently. Additionally, matrices are employed in statistical analysis for organizing and manipulating data, such as in regression analysis and correlation studies.
In physics, matrices are utilized to represent transformations in space, such as rotations and reflections, making them indispensable in computer graphics and animation. In economics, matrices are used to model input-output relationships, equilibrium conditions, and optimization problems in production and consumption.
Furthermore, matrices play a crucial role in network theory, where they represent adjacency matrices for graphs and help analyze connectivity and flow within networks. In operations research and logistics, matrices are employed to optimize resource allocation, scheduling, and routing problems.
Overall, matrices serve as powerful tools for modeling and analyzing complex systems and relationships in diverse contexts, making them essential in both theoretical analysis and practical applications across various disciplines.
To sum up the AP Precalculus Unit 4 review, in the entire overview of AP Precalculus, Unit 4 builds as a lateral support for further courses like Physics and Engineering.



